Specifically, first we explain how to obtain the best investment portfolio with a given target risk. This is important in order to produce portfolios with different risk profiles, as typically offered by financial institutions. Second, we show how to implement individual investment bands, i.e., mini- mum and maximum possible investments for each asset. This is also important in order to impose diversification and avoid corner solutions. Quite remarkably, we show how to build the constrained cost function as a quadratic binary optimization (QUBO) problem, this being the natural input of quantum annealers. The validity of our implementation is proven by finding the optimal portfolios, using D-Wave Hybrid and its Advantage quantum processor, on static portfolios taking assets from S&P100 and S&P500. Our results show how practical daily constraints found in quantitative finance can be implemented in a simple way in current NISQ quantum processors, with real data, and under realistic market conditions. In combination with clustering algorithms, our methods would allow to replicate the behaviour of more complex indexes, such as Nasdaq Composite or others, in turn being particularly useful to build and replicate Exchange Traded Funds (ETF).
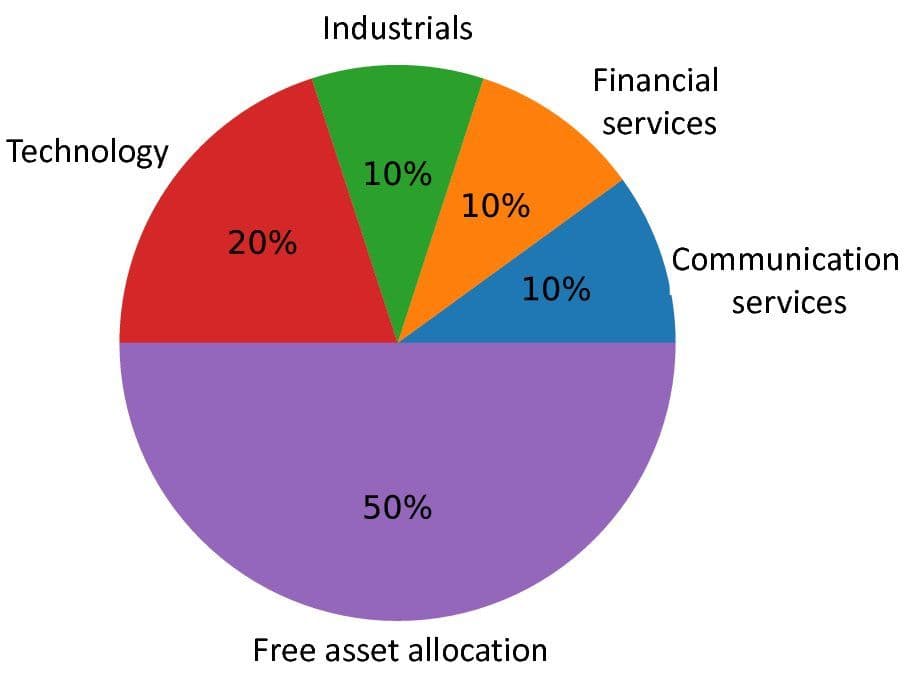
Link to the paper.